Отброс нелицевых граней Алгоритм художника Z-буфер Порталы Z-отсечение Отсечение Отброс нелицевых граней Пусть у нас есть объект, внутри которого камера заведомо не окажется. Обычно такие объекты составляют большую часть или всю сцену. Тогда для каждой грани мы можем увидеть только одну ее сторону - лицевую. Грань - плоскость, она делит все 3D пространство на два полупространства. Так вот, лицевую сторону видно только из одного полупространства, из того, в которое "смотрит" нормаль к этой грани, направленная *из* объекта. Проверив, в какое полупространство попадает камера, можно сразу определить, является ли грань лицевой (то есть, может ли камера увидеть лицевую сторону этой грани) и надо ли ее рисовать. Пусть грань имеет вершины v1, v2, v3 и нормаль (nx,ny,nz). Тогда уравнение плоскости, в которой она лежит, будет иметь вид nx*x+ny*y+nz*z+d = 0. d находим из того факта, что v1 в плоскости лежит: nx*v1.x+ny*v1.y+nz*v1.z+d = 0, d = -(nx*v1.x+ny*v1.y+nz*v1.z). Функция nx*x+ny*y+nz*z+d принимает положительные значения по одну сторону от плоскости, отрицательные по другую и равна нулю на самой плоскости. Точка (v1.x+nx,v1.y+ny,v1.z+nz) лежит, очевидно, в том полупространстве, откуда грань видно. Значение функции (назовем ее функцией видимости) в этой точке равно nx*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)+d = nx*(v1.x+nx)+ny*(v1.y+ny)+nz*(v1.z+nz)-(nx*v1.x+ny*v1.y+nz*v1.z) = nx*nx+ny*ny+nz*nz > 0. Таким образом, если значение функции в какой-то точке больше нуля, то грань из этой точки потенциально видна. Нас интересует видимость грани из нашей камеры, а камера у нас зафиксирована в точке (0,0,-dist). Таким образом, получаем, что грани, для которых -nz*dist-(nx*v1.x+ny*v1.y+nz*v1.z) < 0, или, что равносильно, nz*dist+nx*v1.x+ny*v1.y+nz*v1.z > 0, заведомо не видны и время на их обработку и отрисовку тратить не стоит. Отдельный вопрос - как считать нормали к граням. Точнее, как выбрать одну из двух нормалей, которая будет смотреть из объекта. Обычно эта проблема решается еще на этапе построения 3D моделей - например, пакет 3D Studio записывает вершины граней в порядке A-B-C так, чтобы векторное произведение BA*CA и было нормалью. Еще один способ - выбрать внутренную точку для объекта (либо вручную, либо взять его центр тяжести, либо еще как-нибудь - методов может быть придумано сколько угодно) и использовать ее: если для этой точки функция видимости положительна, то есть грань якобы видна, то надо поменять знак nx, ny и nz. Осталось отметить, что для выпуклых объектов этот метод полностью решает задачу об удалении невидимых частей. Для невыпуклых же он позволяет быстро и просто сократить число граней, подлежащих дальнейшей проверке на видимость и собственно отрисовке. Алгоритм художника Пусть имеется некий набор граней (т.е. сцена), который требуется нарисовать. Отсортируем грани по удаленности от камеры и отрисуем все грани, начиная с самых удаленных. Довольно распространенная характеристика удаленности для грани ABC - это среднее значение z, mid_z = (A.z+B.z+C.z)/3. Вот и весь алгоритм. Просто, и обычно достаточно быстро. Существует, правда, несколько проблем. Во-первых, при некотором расположении граней этот алгоритм вообще не может дать правильного результата - в каком порядке грани не рисуй, получится неправильно. Вот стандартный пример. 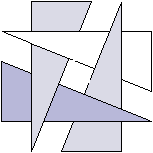Во-вторых, при некотором расположении граней и использовании среднего значения z как характеристики удаленности алгоритм тоже дает неправильный результат. Пример чуть ниже. В этом случае горизонтальную грань надо отрисовывать второй, но по среднему значению z она лежит дальше и таким образом получается, что ее надо отрисовывать первой. Возможные пути решения этой проблемы - какие-то изменения характеристики удаленности, либо моделирование, не вызывающее таких ситуаций. И наконец, при использовании этого алгоритма отрисовываются вообще все грани сцены, и при большом количестве загораживающих друг друга граней мы будем тратить большую часть времени на отрисовку невидимых в конечном итоге частей. То есть совершенно впустую. В таком случае целесообразно использовать какие-то другие методы (например BSP и PVS, порталы, и т.д). Z-буфер Заведем буфер (собственно z-буфер) размером с экран, и забьем его каким-то большим числом, настолько большим, что координаты z для точек сцены заведомо меньше. Например, если z - fixedpoint 16:16, то можно использовать максимально возможное значение, то есть 0x7FFFFFFF. Для каждой рисуемой точки считаем значение z; если оно больше, чем значение в z-буфере (точка закрыта какой-то другой точкой), или меньше, чем -dist (точка находится за камерой), то переходим к следующей точке. Если меньше, то рисуем точку на экране (или в видеобуфере), а в z-буфер записываем текущее значение z. Вот кусок кода для лучшего понимания: // ... if (z > -dist && z < zbuffer[screenX][screenY]) { screen[screenX][screenY] = color; zbuffer[screenX][screenY] = z; } // ... Имеет смысл считать значения не z, а z1 = 1/(z+dist), так как эта величина изменяется по грани линейно, и линейная интерполяция дает точные результаты (более подробно это описано в 4.3). Тогда условия чуть изменяются - точка загорожена другой, если значение z1 *меньше* значения в z-буфере; и точка находится за камерой, если z1 < 0. Буфер инициализируем нулями. Тогда не нежна проверка на положительность z1 - точка попадает в z-буфер и на экран, только если z1 больше текущего значения, и поэтому точки, для которых z1 < 0 в буфер и без проверки никогда не попадут. Код тоже чуть изменится: // ... if (z1 > zbuffer[screenX][screenY]) { screen[screenX][screenY] = color; zbuffer[screenX][screenY] = z1; } // ... Вот и все. Осталось упомянуть, что этот метод иногда называют w-буфером, подчеркивая разницу между хранением z и какой-то обратной величины, w. Это самый простой метод удаления невидимых частей, причем всегда дающий полностью правильные результаты. Единственная проблема - скорость, z-буфер, как самый простой, является и самым медленным методом. Вперед  >>>  1  2  3   8  Комментарии к статье  8 8  Обсудить в чате