Пересечение выпуклых полигонов
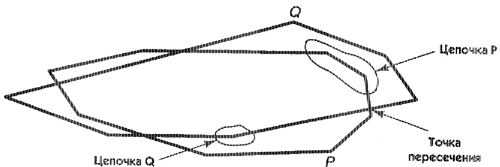
Рассмотрим проблему вычисления области пересечения Р П Q двух выпуклых полигонов Р и Q. За исключением особо оговоренных случаев будем предполагать, что два полигона пересекаются невырожденно: пересечение двух ребер происходит в одной единственной точке, не являющейся вершиной какого-либо полигона. Учитывая такое предположение о невырожденности, всегда получим, что полигон Р П Q состоит из попеременных цепочек из Р и Q. Каждая пара последовательных цепочек соединяется в точке пересечения, в которой пересекаются границы полигонов Р и Q.
 |
Существует несколько решений этой задачи с линейной зависимостью времени выполнения от суммарного числа вершин. Описываемый здесь алгоритм обладает особым изяществом и его легко применять. Для двух заданных на входе выпуклых полигонов Р и Q алгоритм определяет окно на ребре полигона Р и еще одно окно на ребре полигона Q. Идея заключается в продвижении этих окон вдоль границ полигона по мере формирования полигона пересечения Р П Q: окна как бы проталкивают друг друга вдоль границы своих соответствующих полигонов в направлении по часовой стрелке для поиска точек пересечения ребер. Поскольку точки пересечения обнаруживаются в том порядке, в котором они располагаются вокруг полигона Р П Q, полигон пересечения оказывается сформированным, когда некоторая точка пересечения будет обнаружена вторично. В противном случае, если не будет обнаружено ни одной точки пересечения после достаточного числа итераций, то значит границы полигонов не пересекаются. В этом случае потребуется дополнительный простой тест, не содержится ли один полигон внутри другого или они вовсе не пересекаются.
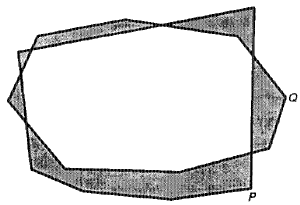 |
Для объяснения работы оказывается весьма полезным ввести понятие серпа. На рисунке справа серпами будут шесть затененных полигонов. Каждый из них ограничен цепочкой, взятой от полигона Р, и цепочкой от полигона Q, ограниченных двумя последовательными точками пересечения. Внутренней цепочкой серпа будет та часть, которая принадлежит полигону пересечения. Отметим, что полигон пересечения окружен четным числом серпов, внутренние цепочки которых попеременно являются частями границ полигонов Р и Q.
В терминах серпов алгоритм поиска полигона пересечения проходит две азы. В процессе первой фазы окно р полигона Р и окно q полигона Q перевещаются в направлении по движению часовой стрелки до тех пор, пока они не будут установлены на ребрах, принадлежащих одновременно одному тому же серпу. Каждое окно начинает свое движение с произвольной позиции. Здесь для краткости будем использовать один и тот же символ р для обозначения как окна полигона Р, так и ребра в этом окне. Тогда термин "начало р" будет относиться к точке начала ребра в окне полигона P, команда "продвинуть р" будет означать, что необходимо переместить окно полигона Р на следующее ребро. Аналогичным образом буквой q будем обозначать как окно полигона Q, так и ребро в окне. Иногда ребра р и q будем читать текущими ребрами.
Во время фазы 2 р и q продолжают перемещаться в направлении по ча-эвой стрелке, но на этот раз они двигаются в унисон от одного серпа к еднему серпу. Перед тем как любое окно перейдет из текущего серпа в седний, ребра р и q пересекутся в точке пересечения, соединяющей оба ерпа. Полигон пересечения строится именно во время второй фазы. Перед каждым перемещением р конечная точка ребра р заносится в полигон перечения, если ребро р принадлежит внутренней цепочке текущего серпа Аналогичным образом перед перемещением q фиксируется конечная точка ребра q, если q принадлежит внутренней цепочке текущего серпа. При кая дом пересечении ребер р и q точка пересечения, в которой они пересекаются, записывается в полигон пересечения.
Для принятия решения, какое из окон должно перемещаться, в алгоря ме используется правило перемещения. Это правило основано на следующв замечаниях: говорят, что ребро а нацелено на ребро b, если бесконечная прямая линия, определяемая ребром b, расположена перед а.
 |
Ребро а нацелено на b, если выполняется одно из условий:
Заметим, что соотношение а х b >= 0 соответствует случаю, при котором угол между векторами a и b меньше 180 градусов
Функция aimsAt возвращает значение TRUE, если и только если ребр а нацелено на ребро b. Параметр aclass указывает на положение конечно точки a.dest относительно ребра b.
Параметр crossType принимает значение COLLINEAR, если и только если ребра а и b коллинеарны.
bool aimsAt (Edge &a, Edge &b, int aclass, int crossType)
{
Point va = a.dest - a.org;
Point vb = b.dest - b.org;
if (crossType != COLLINEAR) {
if ( (va.x * vb.y) >= (vb.x * va.y) )
return (aclass != RIGHT);
else
return (aclass != LEFT);
} else {
return (aclass != BEYOND);
}
}
Если ребра а и b коллинеарны, то ребро а нацелено на b, если конечна точка a.dest не лежит после b. Это обстоятельство используется для тоге чтобы продвинуть а вместо b, когда два ребра пересекаются вырожденно более, чем в одной точке. Позволяя а "догонять" b, мы обеспечиваем, что ни одна точка пересечения не будет пропущена.
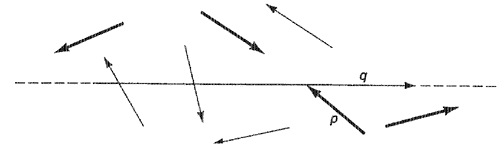
Возвратимся к обсуждению правил перемещения. Они сформулированы таким образом, чтобы не пропустить следующую точку пересечения. Правила отличают текущее ребро, которое может содержать следующую точку пересечения, от текущего ребра, которое возможно не может содержать следующей точки пересечения, причем в этом случае окно переносится вполне безопасно. Правила перемещения различают четыре ситуации, показанные на рис. 4. Здесь ребро а считается находящимся вне ребра b, если конечная точка a.dest расположена слева от b.
 | Четыре правила перемещения:
(а)-продвинуть р; б - продвинуть р,- в - продвинуть р; г - продвинуть р |
р и q нацелены друг на друга: перемещается окно, соответствующее тому ребру (р или q), которое находится снаружи другого. В ситуации рис. 4а должно быть перенесено окно на ребре р. Следующая точка пересечения не может лежать на р, поскольку ребро р находится вне полигона пересечения.
р нацелено на q, но q не нацелено на р: конечная концевая точка ребра р заносится в полигон пересечения, если р не находится снаружи q и затем окно р переносится. На рис. 46 ребро р не может содержать следующей точки пересечения (хотя оно может содержать некоторую точку пересечения, если р находится не снаружи от q). На рис. показана ситуация, в которой ребро р, окно которого должно быть перенесено, не находится снаружи от ребра q.
q нацелено на р, но р не нацелено на q: конечная концевая точка ребра q заносится в полигон пересечения, если q не находится снаружи от р, после чего переносится окно q (рис. 6.14в). Этот случай симметричен предыдущему. На рис. показана ситуация, при которой ребро q, окно которого должно быть перенесено, находится снаружи от ребра Р-
р и q не нацелены друг на друга: переносится то окно, которое относится к ребру, расположенному снаружи от другого. Согласно рис. 4 необходимо перенести окно р, поскольку ребро р находится снаружи от ребра q.
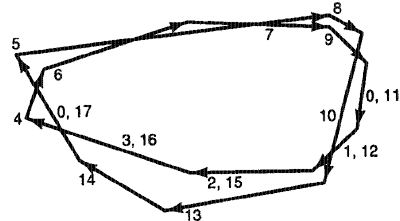
Работа алгоритма показана на рис. 5. Каждое ребро имеет метку i, если оно обрабатывается на шаге i (у некоторых ребер показана двойная метка, поскольку они обрабатываются дважды). Два начальных ребра имеют метку 0. На этом рисунке фаза 2 (когда два текущих ребра оказывал принадлежащими одному и тому же серпу) начинается после трех итераций
Алгоритм реализован в программе convexPolygonlntersect. Програ передаются полигоны Р и Q, она возвращает указатель на резулътирукя полигон пересечения R. Обращение к функции advance использовано переноса одного из двух текущих ребер и для включения конечной конце вой точки ребра в полигон R в соответствии с выполнением определеннь условий. Используются окна, существующие внутри класса Polygon.
enum ( UNKNOWN, P_IS_INSIDE, Q_IS_INSIDE);
Polygon *convexPolygonlntersect(Polygon &P, Polygon &Q)
{
Polygon *R;
Point iPnt, startPnt;
int inflag = UNKNOWN;
int phase = 1;
int maxItns = 2 * (P.size() + Q.size());
// начало цикла for
for (int i = 1; (i<=maxItns) || (phase==2); i++) {
Edge p = P.edge();
Edge q = Q.edge();
int pclass = p.dest.classify (q);
int qclass = q.dest.classify (p);
int crossType = crossingPoint (p, q, iPnt);
if (crossType = SKEW_CROSS) {
if (phase==1) {
phase = 2;
R = new Polygon;
R->insert(iPnt);
startPnt = iPnt;
} else if (iPnt != R->point() ) {
if (iPnt != startPnt)
R->insert(iPnt);
else
return R;
}
if (pclass==RIGHT) inflag = P_IS_INSIDE;
else if (qclass=RIGHT) inflag = Q_IS_INSIDE;
else inflag = UNKNOWN;
} else if ( (crossType-COLLINEAR) && (pclass != BEHIND) && (qclass ! = BEHIND) )
inflag = UNKNOWN;
bool pAIMSq = aimsAt(p, q, pclass, crossType);
bool qAIMSp = aimsAt(q, p, qclass, crossType);
if (pAIMSq && qAIMSp) {
if ( (inflag == Q_IS_INSIDE) || ( (inflag == UNKNOWN) && (pclass == LEFT)))
advance(P, *R, FALSE);
else
advance (Q, *R, FALSE);
} else if (pAIMSq) {
advance (P, *R, inflag == P_IS_INSIDE);
} else if (qAIMSp) {
advance (Q, *R, inflag == Q_IS_INSIDE);
} else {
if ((inflag == Q_IS_INSIDE) ((inflag == UNKNOWN) && (pclass == LEFT)))
advance ( P , *R , FALSE );
else
advance (Q, *R, FALSE);
}
}
// конец цикла for
if (pointInConvexPolygon ( P.point (), Q) )
return new Polygon (P);
else if (pointInConvexPolygon (Q.point(), P) )
return new Polygon(Q);
return new Polygon;
}
Если после выполнения 2(|Р| + |Q|) итераций не будет обнаружено ни одной точки пересечения, то основной цикл завершается, поскольку это означает, что границы полигона не пересекаются. Последующие обращения к функции pointlnConvexPolygon производятся с целью обнаружения ситуаций Р С Q, Q П Р или Р П Q = 0. В противном случае, если найдена некоторая точка пересечения iPnt, то алгоритм продолжает построение полигона пересечения R и останавливается только после того, как точка iPnt будет обнаружена вторично.
Переменная inflag показывает, какой из двух входных полигонов находится в данный момент внутри другого - т. е. указывает на полигон, текущее ребро которого находится в составе внутренней цепочки текущего серпа. Более того, переменная inflag принимает значение UNKNOWN (неизвестно) во время первой фазы, а также всякий раз, когда оба текущих ребра коллинеарны или перекрывают друг друга. Значение этой переменной меняется при каждом обнаружении новой точки пересечения.
Процедура advance продвигает текущее ребро полигона А, представляющее либо Р, либо Q. Эта же процедура заносит конечную концевую точку ребра х в полигон пересечения R, если А находится внутри другого полигона и * не была последней точкой, записанной в R:
void advance (Polygon &A, Polygon &R, int inside)
{
A. advance (CLOCKWISE);
if (inside && (R.point() != A.point ()))
R.insert (A.point());
}
1 2 3
8 8 8
| |