Анализ и корректность Доказательство корректности показывает наиболее важные моменты ра боты алгоритма - один и тот же набор правил продвижения работает течение обеих фаз. Правило продвижения заносит р и q в один и тот на серп и затем передвигает р и q в унисон из одного серпа в другой. Корректность алгоритма следует из двух утверждений: Если текущие ребра р к q принадлежат одному и тому же серпу, тогда можно будет найти следующую точку пересечения, в которой закаа чивается текущий серп, и эта точка будет именно следующей. Если границы полигонов Р и Q пересекаются, то текущие ребра р и пересекутся в некоторой точке пересечения после не более, чем 2(|Р| + |Q|) итераций. Утверждение 2 обеспечивает, что алгоритм найдет некоторую точку пересечения, если таковая существует. Поскольку ребра р и q принадлежат одному и тому же серпу, если они пересекаются, то из утверждения 1 следует, что остальные точки пересечения будут найдены в нужном порядке. 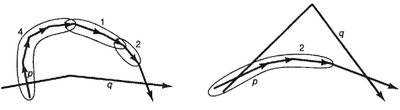Рассмотрим сначала утверждение 1. Предположим, что р и q принадлежат одному и тому же серпу и q достигает некоторой точки пересечения раньше, чем р. Мы покажем, что тогда q останется неподвижным, пока не достигнет точки пересечения после ряда последовательных продвижений Могут возникнуть две ситуации. Сначала предположим, что р нахрдится снаружи от q (рис. ниже). При этом q останется фиксированным, пока будет продвигаться согласно нулю или нескольким применениям правила 4 затем нулю или нескольким применениям правила 1 и потом нулю или нескольким применениям правила 2. Во второй ситуации предположим, что р не находится снаружи от q (рис. ниже ). Здесь q будет оставаться фиксированным, пока р будет продвигаться путем нуля или нескольких применений правила 2. В симметричной ситуации, когда р достигает точки пересечения раньше, чем q, ребро q остается фиксированным, а ребро q продвигается до точки встречи. Это можно показать аналогичным образом, только меняется роль р и q и правило 3 заменяет правило 2. Из этого следует утверждение 1. Чтобы показать утверждение 2, предположим, что границы Р и Q пересекаются. После |Р| + |Q| итераций либо р, либо q должны совершить полный оборот вокруг своего полигона. Предположим, что это произошло с р. В некоторый момент времени ребро р должно расположиться так, что оно будет содержать точку пересечения, в которой полигон Q переходит извне полигона Р внутрь его. Это происходит потому, что существуют по крайней мере две точки пересечения и направление пересечения меняется. Пусть q будет ребром внутри окна полигона Q в момент обнаружения такого р. 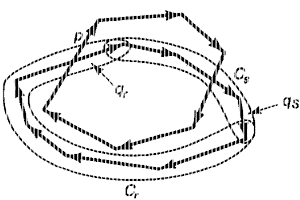На рисунке ниже граница полигона Q разбита на две цепочки Сr и Cs. Первая цепочка Сr заканчивается в ребре qr, в том ребре полигона Q, которое входит внутрь полигона Р через его ребро р. Другая цепочка Cs заканчивается в ребре qs, конечная точка которого лежит справа от бесконечной прямой линии, определяемой ребром р, и она наиболее удалена от этой прямой линии. Следует рассмотреть два случая в зависимости от того, какой из двух цепочек принадлежит ребро q: Случай 1 [q принадлежит Сr]. Здесь р остается фиксированным, тогда как q продвигается согласно нулю или нескольким применениям правила 3, затем правила 4, потом правила 1 и, наконец, правила 3, когда обнаруживается точка пересечения. Случай 2 [qi принадлежит Сr]. Здесь q остается фиксированным, а р продвигается согласно нулю или нескольких применений правила 2, затем правила 4, потом оравила 1 и, наконец, правила 2 в момент, когда р окажется внутри q. С этого момента оба ребра р и q могут продвигаться несколько раз, однако ребро q не может быть продвинуто за его следующую точку пересечения, пока р сначала не достигнет предыдущей точки пересечения ребра q (если этого уже не произошло с ребром р). Поскольку р и q заканчиваются в одном и том же серпе, утверждение 1 гарантирует, что после некоторого числа дополнительных продвижений они пересекутся в точке пересечения, в которой заканчивается текущий серп. Чтобы показать, что достаточно 2(|Р| + |Q|) итераций для поиска некоторой точки пересечения, заметим, что при доказательстве утверждения 2 (о том, что граница полигона Q входит внутрь полигона Р через ребро р при произвольном положении ребрв q) начальные позиции р и q достигались при выполнении не более |Р| + |Q| итераций. Фактически такая ситуация, либо симметричная ей, в оторой роли р и q взаимно заменяются, достигается за меньшее число итераций. Поскольку после этого ни р, ни q не будут продвинуты на полный оборот прежде, чем будет достигнута первая точка пересечения, потребуется не более |Р| + |Q| дополнительных продвижений. <<<  Назад Вперед  >>>  1  2  3   8  Комментарии к статье  8 8  Обсудить в чате