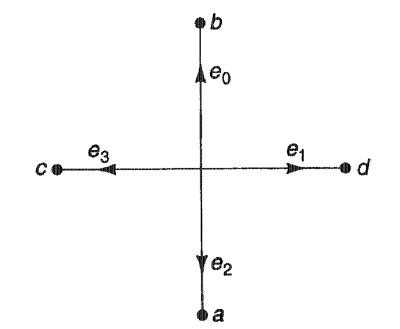
Ребра Класс Edge (Ребро, любые линии) Поворот ребер Определение точки пересечения двух прямых линий Расстояние от точки до прямой линии Дополнительные утилиты Множество геометрических алгоритмов затрагивает прямые линии в той или иной форме. Отрезок прямой линии p0p1 состоит из двух концевых точек р0 и p1 вместе с точками, лежащими между ними. Когда важен порядок следования точек р0 и p1, то мы говорим о направленном отрезке прямой линии р0р1. Концевая точка р0 является началом направленного отрезка прямой линии, а точка p1 - его концом. Обычно направленный отрезок прямой линии будем называть ребром, если он представляет собой сторону некоторого полигона. Ребро направлено таким образом, что внутренняя часть полигона располагается всегда справа от него. Бесконечная (направленная) прямая линия определяется двумя точками и направлена от первой точки ко второй. Луч является полубесконечной прямой линией, начинающейся в точке начала и проходящей через вторую точку. Класс Edge (Ребро, любые линии) Класс Edge, применяется для представления всех форм прямых линий. Он определяется следующим образом: class Edge { public: Point org; Point dest; Edge (Point &_org, Point &_dest); Edge (void); Edge &rot (void); Edge &flip (void); Point point (double); int intersect (Edge&, double&); int cross (Edge&, double&); bool isVertical(void); double slope(void); double у(double); }; Концевые точки начала и конца хранятся в элементах данных org и dest соответственно. Эти элементы инициализируются конструктором Edge: Edge::Edge (Point &_org, Point &_dest) : org (_org), dest (_dest) { } Полезно также иметь конструктор для класса Edge, не требующий аргументов: Edge::Edge (void) : org (Point (0,0)), dest (Point (1,0)) { } Поворот ребер Под термином поворот ребра подразумевается вращение ребра на 90 градусов в направлении по часовой стрелке вокруг его средней точки. Два последовательных поворота ребра приводят к его перевороту, поскольку при этом происходит смена направления ребра на противоположное. Три последовательных поворота ребра соответствуют повороту ребра на 90 градусов в направлении против движения часовой стрелки вокруг его середины. Четыре последовательных поворота оставляют ребро неизменным. 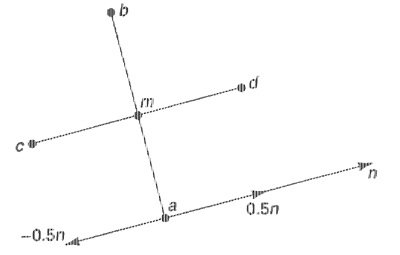На рисунке ниже показано, как путем поворота ребра ab формируется ребро ca. Если вектор b - а = (х, у), то вектор n, перпендикулярный вектору b - а, определяется как n = (у, -х). Средняя точка m между точками а и b определяется как m = (а + b)/2. Тогда точки с и d определяются как с = m - n/2 и d = m + n/2. Поворот реализуется компонентной функцией rot следующим образом: Edge &Edge::rot(void) { Point m = 0.5 * (org + dest); Point v = dest - org; Point n(v.у, -v.x); org = m - 0.5 * n; dest = m + 0.5 * n; return *this; } Заметим, что функция rot является разрушающей. Она изменяет текущее ребро вместо того, чтобы формировать новое ребро. Функция возвращает ссылку на текущее ребро, поэтому обращение к функции rot может стоять непосредственно в более сложных выражениях. Это позволяет, например, записать следующее краткое определение компонентной функции flip для изменения направления текущего ребра на обратное: Edge &Edge::flip(void) { return rot().rot(); } При таком определении компонентной функции flip первое обращение к функции rot (слева от оператора доступа к элементу) поворачивает текущее ребро, а затем второе обращение поворачивает его еще раз. Определение точки пересечения двух прямых линий Бесконечная прямая линия ab, проходящая через две точки а и b, может быть записана в параметрической форме как P(t) = a +t(b - a)      (1) где параметр t может принимать любое значение в диапазоне вещественных чисел (если значения t ограничены диапазоном 0 <= t <= 1, то уравнение (1) описывает отрезок прямой линии аb). Параметрическая форма описания прямой линии устанавливает соответствие между вещественными числами и точками на прямой линии. На рисунке ниже показаны точки на прямой линии, соответствующие различным значениям параметра t. Компонентные функции Edge::intersect и Edge::point предусмотрены для совместной работы при поиске точки пересечения двух бесконечных прямых линий е и f. Если е и f являются объектами класса Edge, то фрагмент программы double t; Point p; if (e.intersect(f,t) = SKEW) p = e.point(t) Oпределяет t как параметрическое значение (вдоль прямой линии е) точки, в которой пересекаются прямые линии е и f и затем эта точка р становится текущей точкой. Функция intersect возвращает значения типа перечисления: SKEW (наклон), если прямые линии пересекаются в некоторой точке, COLLINEAR, если прямые линии коллинеарны, или PARALLEL, если они параллельны. Компонентная функция point обрабатывает параметрическое значение t и возвращает соответствующую точку. Задача решается обращением к двум координатным функциям вместо обращения к одной общей функции, поскольку иногда нам достаточно определить параметрическое значение точки пересечения, а не саму точку пересечения. Реализация компонентной функции point очень проста - значение параметра t подставляется в параметрическое уравнение для этой линии: Point Edge::point(double t) { return Point(org + t * (dest - org)); } Реализация компонентной функции intersect основана на записи скалярного произведения а * b для двух векторов а = (ха, уа) и b = (хb, уb), которое определяется как а * b = хaхb + yayb. Скалярное произведение имеет несколько важных свойств, включая основные: Если a, b и с - векторы, то a * b = b * а и а * (b + с) = а * b + а * с = (b + с) * а. Если s - скаляр, то (sa) * b = s(a * b) и a * (sb) = s(a * b). Если а - нулевой вектор, то a * a = 0, в противном случае a * a > 0. ||a|| = а * а. На основании этих основных свойств можно получить очень важное свойство, на котором основан целый ряд операций с прямыми линиями: два вектора а и b перпендикулярны, если, и только если их скалярное произведение равно нулю a * b = 0. Вообще говоря, имеет место следующая теорема: Пусть a и b - векторы, Theta - угол между ними. Тогда {>} {>} a * b {=} 0, если и только если Theta {=} 90 градусов. {<} {<} Теорема о скалярном произведении может быть использована для нахождения точки пересечения двух прямых линий ab и cd. Если прямая линия ab описывается уравнением P(t) = а + t(b - а), то будем искать значение t такое, что прямые линии аb и cd пересекаются в точке P(t). Поскольку вектор P(t)-с должен совпадать с прямой линией cd, то и вектор P(t)-с и прямая линия cd должны быть перпендикулярны одному и тому же вектору n. Следовательно, на основании теоремы о скалярном произведении нам необходимо решить относительно t уравнение n * ( P(t)-c ) = 0     (2) Поскольку P(t) = а + t(b - а), уравнение (2) можно переписать в виде n * ((a + t (b - а)) - с) = 0 Учитывая основные свойства скалярного произведения, получим n * (а - с) + n * (t(b - a)) = 0 Выводя за скобки параметр t, имеем n * (а - с) + t[(n * (b - a)] = 0 Откуда следует n * (a-c) t=  --   ==========,    n * (b-a) =/= 0     (3) n * (b-a) Уравнение (3) удовлетворяется, если и только если бесконечные прямые линии аb и cd не параллельны и они пересекаются в единственной точке. Если две прямые линии параллельны или совпадают, то этот факт соответствует выполнению условия n * (b - а) = 0, поскольку оба вектора (b - а) и (d - с) перпендикулярны одному и тому же вектору п. В результате получаем следующую реализацию компонентной функции intersect: enum { COLLINEAR, PARALLEL, SKEW, SKEW_CROSS, SKEW_NO_CROSS }; int Edge::intersect(Edge &e, double &t) { Point a = org; Point b = dest; Point с = e.org; Point d = e.dest; Point n = Point((d-c).y, (c-d).x); double denom = dotProduct(n, b-a); if (denom ==0.0) { int aclass = org.classify(e); if ((aclass==LEFT) || (aclass==RIGHT)) return PARALLEL; else return COLLINEAR; } double num = dotProduct(n, a-c); t = -num / denom; return SKEW; } Реализация функции dotProduct (скалярное произведение) очень проста: double dotProduct(Point &p, Point &q) { return (p.x * q.x + p.у * q.y); } Компонентная функция Edge::cross возвращает значение SKEW_CROSS (наклонены, и пересекаются), если и только если текущий отрезок прямой линии пересекает отрезок прямой линии е. Если отрезки прямой линии пересекаются, то возвращается значение параметра t вдоль этого отрезка прямой линии, соответствующее точке пересечения. В противном случае функция возвращает одно из следующих подходящих значений COLLINEAR (коллинеарны) , PARALLEL (параллельны) или SKEW_NO_CROSS (наклонены, но без пересечения). int Edge::cross(Edge &e, double &t) { double s; int crossType = e.intersect(*this, s); if ((crossType==COLLINEAR) || (crossType==PARALLEL)) return crossType; if ((s < 0.0) || (s > 1.0)) return SKEW_NO_CROSS; intersect(e, t); if ((0.0 <= t) && (t <= 1.0)) return SKEW_CROSS; else return SKEW_NO_CROSS; } Расстояние от точки до прямой линии Определение функции Point::distance иллюстрирует некоторые иа только что описанных свойств. В эту компонентную функцию класса Point передается ребро е и возвращается значение расстояния от текущей точка до ребра е со знаком. Здесь под термином расстояние от точки р до ребра е понимается минимальное расстояние от точки р до некоторой точки на бесконечной прямой линии, определяемой ребром е. Расстояние со знакол будет положительным, если точка р лежит справа от ребра е, отрицательным, если точка р лежит слева от ребра е, либо нулевым, если точка принадлежит прямой линии. Компонентная функция distance определяется следующим образом: double Point::distance(Edge &e) { Edge ab = e; ab.flip().rot(); // поворот ab на 90 градусов // против часовой стрелки Point n(ab.dest - ab.org); // n = вектор, перпендикулярный ребру е n = (1.0 / n.length()) * n; // нормализация вектора n Edge f(*this, *this + n); // ребро f = n позиционируется // на текущей точке double t; // t = расстоянию со знаком f.intersect(e, t); // вдоль вектора f до точки, // в которой ребро f пересекает ребро е return t; } В функции сначала формируется единичный вектор n такой, что он перпендикулярен ребру е и направлен влево от ребра е. Затем вектор n переносится до совпадения его начала с текущей точкой, образуя ребро f. И, наконец, вычисляется параметрическое значение точки пересечения ребра f с ребром е. Поскольку ребро f перпендикулярно ребру е, имеет единичную длину и начинается в текущей точке, то параметрическое значение t точки пересечения равно расстоянию со знаком от текущей точки до ребра е. Дополнительные утилиты Последние три компонентные функции класса Edge введены для удобства. Компонентная функция isVertical возвращает значение TRUE (истина) только в том случае, если текущее ребро вертикально: bool Edge::isVertical(void) { return (org.x == dest.x); } Компонентная функция slope возвращает величину наклона текущего ребра или значение DBL_MAX, если текущее ребро вертикально: double Edge::slope(void) { if (org.x != dest.x) return (dest.y - org.y) / (dest.x - org.x); return DBL MAX; } Для компонентной функции у задается значение х и она возвращает значение у, соответствующее точке (х, у) на текущей бесконечной прямой линии. Функция действует только в том случае, если текущее ребро не вертикально. double Edge::у(double x) { return slope() * (х - org.x) + org.y; } <<<  Назад  1  2  3  4   8  Комментарии к статье  8 8  Обсудить в чате