Аффинное Этот метод текстурирования основан на приближении u, v линейными функциями. Итак, пусть u - линейная функция, u = k1*sx+k2*sy+k3. Можно посчитать k1, k2, k3 исходя из того, что хотя бы в вершинах грани u должно совпадать с точным значением - это даст нам три уравнения, из которых быстро и просто находятся эти коэффициенты, и потом считать u по этой формуле. Но это все равно медленно - два умножения на пиксел. 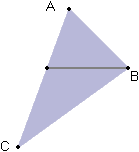Будем рисовать грань по строкам - это общепринято, довольно просто, и не доводит до умопомешательства кэш-память процессора. Вершины грани заранее отсортируем по sy (например, A.sy <= B.sy <= C.sy). Для каждой строки можно посчитать начальное значение x, u (так же, как и для x, ведь u по любой прямой меняется тоже линейно), а также длину этой строки. В нарисованном случае, например, x_start = A.sx+(current_sy-A.sy)*(C.sx-A.sx)/(C.sy-A.sy), u_start = A.u+(current_sy-A.sy)*(C.u-A.u)/(C.sy-A.sy), x_end = A.sx+(current_sy-B.sy)*(B.sx-A.sx)/(B.sy-A.sy), length = x_end - x_start. Какие вершины использовать в этих формулах - это уже проблемы рисования треугольника, а не текстурирования. Лично я просто храню x_start, x_end, u_start, на каждом переходе вниз на строчку прибавляю к delta_x_start = (C.sx-A.sx)/(C.sy-A.sy), и аналогично высчитываемые приращения для x_end, u_start. Вот только надо аккуратно следить за тем, какая сторона правая, какая - левая, и на каком мы сейчас промежутке находимся - то ли AB, то ли BC, и соответственно изменять приращения. Впрочем, все это - уже обыкновенное рисование треугольника. В примерах просто сделано решение "в лоб" - проверяем, какой участок - AB или BC - пересекает текущая строка, считаем x/u/v на обоих концах, считаем длину строки и берем соответствующие левому концу (то есть меньшему x) значения u и v. Так вот. Посчитали начало строки, длину строки, u в начале строки. Осталось заметить, что раз уж u = k1*sx+k2*sy+k3, то при переходе к следующему пикселу строки у нас u изменяется на k1 (так же известный как du/dsx). Это число и надо как-то посчитать. Например, так: x_start = A.sx+(B.sy-A.sy)*(C.sx-A.sx)/(C.sy-A.sy), x_end = B.sx, u_start = A.u+(B.sy-A.sy)*(C.u-A.u)/(C.sy-A.sy), u_end = B.u, du_dsx = (u_start-u_end)/(x_start-x_end). du/dsx - просто число, оно не меняется на всем треугольнике, поэтому просто считаем его там, где удобно, и берем посчитанное значение. v (из тех же соображений) считается абсолютно точно так же, надо только во всех приведенных формулах u заменить на v, и все. Теперь осталось только взять и нарисовать эту строку: // ... u = u_start; v = v_start; for (current_sx = x_start; current_sx <= x_end; current_sx++) { putpixel(current_sx, current_sy, texture[(int)v][(int)u]); u += du_dsx; v += dv_dsx; } // ... Пройдясь по всем строкам грани - т.е. пробежавшись current_sy по значениям от A.sy до C.sy (вершины отсортированы!), получим текстурированную грань. Voila! <<<  Назад Вперед  >>>  1  2  3  4  5  6   8  Комментарии к статье  8 8  Обсудить в чате