8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
|
 |
Распределение Пуассона - Программирование от RIN.RU
|
Распределение Пуассона
| Обозначение | 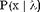 | | Область значений | x - целое, 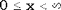 | | Параметры | Параметр положения  | | Плотность (функция вероятности) | 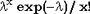 | | Математическое ожидание | 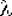 | | Дисперсия | 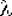 | | Функция распределения | 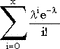 |
Связь с другими распределениями
Вероятность того, что пуассонова случайная величина не превосходит x, равна вероятности того, что случайная величина, имеющая распределение хи-квадрат с 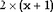 степенями свободы, больше степенями свободы, больше 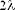 : :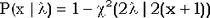 . Поскольку хи-квадрат, в свою очередь, является частным случаем гамма-распределения, получаем . Поскольку хи-квадрат, в свою очередь, является частным случаем гамма-распределения, получаем 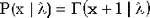 . Конечно, к этому заключению можно было придти и непосредственно. . Конечно, к этому заключению можно было придти и непосредственно.
Сумма n независимых случайных величин,  , i=1..n, где , i=1..n, где  подчиняется распределению Пуассона с параметром подчиняется распределению Пуассона с параметром 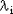 , имеет также распределение Пуассона с параметром , имеет также распределение Пуассона с параметром 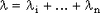 . .
Распределение Пуассона является предельной формой биномиального распределения 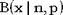 при при 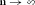 , , 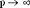 , , 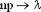 . .
При 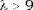 распределение Пуассона можно аппроксимировать нормальным распределением со средним и дисперсией, равными распределение Пуассона можно аппроксимировать нормальным распределением со средним и дисперсией, равными 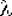 . .
Генерация случайных чисел
Простой способ мне не известен. Вот трудоемкий:
Вычисляем функцию распределения 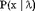 , x=0..N где N произвольно, но достаточно велико (величина этого "велико" зависит от величины , x=0..N где N произвольно, но достаточно велико (величина этого "велико" зависит от величины 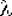 ). Положим ). Положим 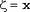 , если , если 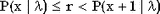 , где r подчиняется равномерному на [0,1] распределению. , где r подчиняется равномерному на [0,1] распределению.
Поскольку вычислять функцию распределения бывает накладно, при малых 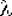 можно применять следующий метод: можно применять следующий метод: 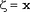 , если , если 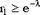 , ,  , :, , :, 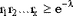 , , 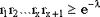 . .
Вычисление функции распределения и ее квантилей
Конечно, при вычислении кумулятивной функции распределения следует воспользоваться упомянутой связью пуассоновского и гамма-распределения (см. функцию poissonDF). Этот способ заведомо лучше непосредственного суммирования уже при n = 10.
Как всегда, когда мы имеем дело с дискретной функцией распределения, вычисление квантилей неосмысленно; при проверке статистических критериев предлагается сравнивать с заданным порогом наблюденные значимости.
Взамен приводится функция rev_poissonDF, которая по известной вероятности y того, что случайная величина, подчиняющаяся распределению Пуассона, не превосходит n, находит параметр 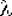 этого распределения. Другими словами, эта функция применяется для решения по этого распределения. Другими словами, эта функция применяется для решения по 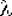 уравнения уравнения  . .
Она полезна, например, для определения левой и правой границ доверительного интервала.
1 2
8 8 8
| |
|
|








