Терминология и обозначения
Пусть дана случайная величина X с областью значений RX (иногда ее называют спектром). Здесь рассматриваются лишь два типа спектров:
совокупность действительных чисел - вся, или луч [0,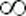 ), или отрезок [a,b]; ), или отрезок [a,b];
совокупность целых чисел - вся, или лишь натуральные числа, или отрезок натуральных чисел от 0 до n.
Когда спектром случайной величины является подмножество действительных чисел, ее называют непрерывной. Если же спектр - подмножество целых чисел, случайная величина дискретна.
Функция распределения F случайной величины X определяется равенством
F(x) = Pr{X < x}, где x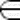 RX, F(x) RX, F(x)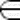 [0,1]. [0,1].
Легко убедиться в том, что F(x) не убывает. Как правило, функцию распределения непрерывной случайной величины саму называют непрерывной, то же и для дискретной.
Функции распределений всех непрерывных случайных величин, встречающихся в стандартных статистических моделях, непрерывно дифференцируемы. Производная f(x), если она существует, называется плотностью вероятности. Дискретная случайная величина принимает дискретные значения x с вероятностями f(x). Функция f(x) в этом случае называется функцией вероятности, а иногда - функцией массы.
Значение x, для которого F(x) = p, называется p-квантилем (впрочем, для этого термина используется и женский род). Функция G(p), ставящая в соответствие каждому p из [0,1] квантиль x из RX, называется обратной функцией распределения. Обратите внимание на некоторые трудности, возникающие при вычислении квантилей дискретных случайный величин; лично я предпочитаю в подобных случаях самое правое из тех x, для которых F(x) = p. Кроме того, квантили дискретных функций распределения существуют не для всех p, что вызывает известные трудности при построении критериев проверки статистических гипотез.
Содержание
В этом справочнике рассмотрены наиболее часто встречающиеся одномерные распределения: для каждого приведено определение, а также среднее и дисперсия, если они выражаются через элементарные функции. Во всех сколько-нибудь нетривиальных случаях указывается также способ вычисления самой функции распределения и ее квантилей. Кроме того, приводятся способы генерации (псевдо)случайных чисел, подчиняющихся рассматриваемым распределениям.
Отдельно следует сказать о приводимых кодах на С++. Прежде всего, эти коды принимает MSVC v.6; я надеюсь, что их без проблем 'сглотнут' и другие компиляторы. Реализованные методы вычисления я довольно давно использую в своей статистической практике; во всех задачах, с которыми я сталкивался, они оказались работоспособными. Тем не менее, коды предназначены служить лишь как иллюстрацией того, как можно реализовать вычисления. В 'боевой' обстановке следует использовать специальные библиотеки, тщательно спланированные и адекватно тестированные.
Неисчерпаемым источником идей и методов генерации случайных чисел является глава "Получисленные алгоритмы" из второго тома великой работы Д.Кнута "Искусство программирования для ЭВМ" (D.E.Knuth, The Art of Computer Programming, v.2, ch.3: "Seminumerical Algorithms").
Конечно, имеется достаточно много специализированных библиотек с функциями, генерирующими случайные числа, проверяющими их и т.д. и т.п. Примером может служить библиотека randlib, содержащая генераторы случайных чисел для основных распределений, имеется в двух версиях - на Си и на Фортране. Довольно старомодные коды, которые зато дают довольно хорошие числа.
8 8 8
| |








