Подход 1 Будем рассматривать нашу задачу из системы координат с началом в центре первой окружности. Определить центр окружности по каноническому уравнению вида Ax2 + Ay2 + a1x + a2y + a0 = 0, где A =/= 0, довольно просто - это (-a1/2A, -a2/2A); перенести систему координат можно простым преобразованием Xстарое=Xновое - a1/2A Yстарое=Yновое - a2/2A - подставить вместо старых переменных их новые значения в уравнения. В такой системе координат уравнения окружностей можно записать как (1) x2 + y2 = R2 (2)(x-a)2 + (y-b)2 = r2 Раскрывая скобки, вычитая (1) из (2) и приводя подобные, получаем другой вид (2): -2ax-2by = R2 - r2 - a2 - b2. Если еще упростить и немного поменять обозначения, то (2) приведется к виду ax+by=C, где С - новое обозначение выражения справа. Таким образом, имеем систему: (1) x2 + y2 = R2 (2) ax + by = C, решение которой, надеюсь, не составит проблем (например, подойдет подстановка - естественно с учетом случаев a=0, b=0 и т.п.) (2) в (1) и имеем простое квадратное уравнение на одну из переменных. Решив его и получив из (2) значение оставшейся переменной, имеем(если и только если она есть) точку пересечения. 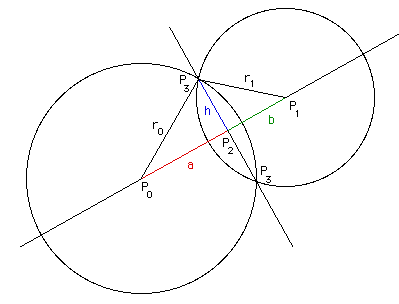Подход 2 Пусть нужно найти пару точек P3 пересечения, если они существуют. Для начала найдем расстояние между центрами окружностей. d = || P1 - P0 ||. Если d > r0 + r1, тогда решений нет: круги лежат отдельно. Аналогично в случае d < || r0 - r1 || - тогда нет решений, так как одна окружность находится внутри другой. Рассмотрим два треугольника P0P2P3 и P1P2P3. Имеем a2 + h2 = r02 and b2 + h2 = r12 Используя равенство d = a + b, мы можем разрешить относительно a: a = (r02 - r12 + d2 ) / (2 d) В случае соприкосновения окружностей, это, очевидно, превратится в r0, так как: d = r0 + r1 Решим относительно h, подставив в первое уравнение h2 = r02 - a2 Итак, P2 = P0 + a ( P1 - P0 ) / d Таким образом, получаем координаты точек P3 = (x3,y3): x3 = x2 +- h ( y1 - y0 ) / d y3 = y2 -+ h ( x1 - x0 ) / d  8  Комментарии к статье  8 8  Обсудить в чате