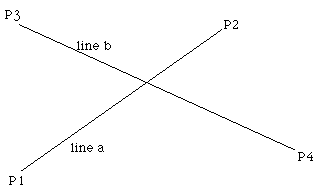
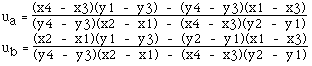Уравнения линий имеют вид Pa = P1 + ua ( P2 - P1 ) Pb = P3 + ub ( P4 - P3 ) Решение относительно точки Pa = Pb дает два уравнения на координаты (ua и ub) x1 + ua (x2 - x1) = x3 + ub (x4 - x3) и y1 + ua (y2 - y1) = y3 + ub (y4 - y3) Решая относительно ua и ub имеем Подстановка любого из этих значений в соответствующее уравнение прямой даст точку пересечения. Пусть, например, точка пересечения (x,y): x = x1 + ua (x2 - x1) y = y1 + ua (y2 - y1) Замечания Знаменатели одинаковы. Если знаменатель равен нулю, то прямые параллельны. Если и числитель и знаменатель равны нулю, то прямые совпадают. Если нужно найти пересечение отрезков, то нужно лишь проверить, лежат ли ua и ub на промежутке [0,1]. Если какая-нибудь из этих двух переменных 0 <= ui <= 1, то соответствующий отрезок содержит точку пересечения. Если обе переменные приняли значения из [0,1], то точка пересечения прямых лежит внутри обоих отрезков. Для двух отрезков при достаточной разреженности объектов можно сначала проверять принципиальную возможность пересечения, сравнивая координаты концов. Пример реализации от Shadow BOOL IsLinesCross(_int64 x11, _int64 y11, _int64 x12, _int64 y12, _int64 x21, _int64 y21, _int64 x22, _int64 y22) { _int64 maxx1 = max(x11, x12), maxy1 = max(y11, y12); _int64 minx1 = min(x11, x12), miny1 = min(y11, y12); _int64 maxx2 = max(x21, x22), maxy2 = max(y21, y22); _int64 minx2 = min(x21, x22), miny2 = min(y21, y22); if (minx1 > maxx2 || maxx1 < minx2 || miny1 > maxy2 || maxy1 < miny2) return FALSE; // Момент, када линии имеют одну общую вершину... _int64 dx1 = x12-x11, dy1 = y12-y11; // Длина проекций первой линии на ось x и y _int64 dx2 = x22-x21, dy2 = y22-y21; // Длина проекций второй линии на ось x и y _int64 dxx = x11-x21, dyy = y11-y21; _int64 div, mul; if ((div = (_int64)((double)dy2*dx1-(double)dx2*dy1)) == 0) return FALSE; // Линии параллельны... if (div > 0) { if ((mul = (_int64)((double)dx1*dyy-(double)dy1*dxx)) < 0 || mul > div) return FALSE; // Первый отрезок пересекается за своими границами... if ((mul = (_int64)((double)dx2*dyy-(double)dy2*dxx)) < 0 || mul > div) return FALSE; // Второй отрезок пересекается за своими границами... } if ((mul = -(_int64)((double)dx1*dyy-(double)dy1*dxx)) < 0 || mul > -div) return FALSE; // Первый отрезок пересекается за своими границами... if ((mul = -(_int64)((double)dx2*dyy-(double)dy2*dxx)) < 0 || mul > -div) return FALSE; // Второй отрезок пересекается за своими границами... return TRUE; }  8  Комментарии к статье  8 8  Обсудить в чате