Более эффективный способ решения этой задачи использует построение суффиксного дерева, представляющего текст, где производится поиск. Описание этой структуры данных было приведено в предыдущем разделе, ниже мы повторим его основные моменты. Затем последует описание алгоритма суффиксного дерева Мак-Крейта (McCreight), и наконец, будет рассмотрен способ использования этого дерева для данной задачи.
Будем считать, что данная строка текста завершается специальным маркером конца $, который больше нигде в строке не появляется. Если это не так, подобный символ можно просто приписать к y справа. Суффиксное дерево для y имеет n листьев, каждый из которых представляет один из суффиксов y(i, n), 1 < i < n, строки y. Степени всех внутренних узлов > 2, узлы представляют самые длинные общие префиксы суффиксов y. Два узла, представляющие подстроку b строки y и собственный префикс a этой строки, соединяются ребром, только если не существует узла, представляющего подстроку y, скажем, c, такую, что с является собственным префиксом b, а a - собственным префиксом c. С каждым ребром связана подстрока, добавление которой к подстроке ее исходного узла в результате дает подстроку, представляемую ее узлом назначения. Таким образом, подстроки, представляемые ребрами одного уровня (sibling), должны начинаться с разных символов. Приведенные выше требования гарантируют, что суффиксное дерево для данной строки единственно с точностью до изоморфизма графов.
Способ построения суффиксного дерева, которое МакКрейт [McCreight, 1976] называет 'Алгоритмом M', приводит к структуре данных, функционально эквивалентной индексу подстроки Вейнера [Weiner, 1973]. Она, однако, более эффективно расходует память, чем исходная, и описание версии этого алгоритма приведено ниже.
Пусть Y - суффиксное дерево для строки y. Далее, пусть Yi представляет дерево на i-м этапе его построения. Y0 - это пустое дерево, которое содержит только корневой узел. Дерево можно построить, добавляя по одному соответствующие суффиксам y пути, начиная с самого длинного, и заканчивая самым коротким, то есть суффиксы y(i, n) для 1 < i < n. Таким образом, имеется следующий процесс, в котором операция insert вставляет путь, соответствующий суффиксу y(i, n) в дерево Yi-1:
for i = 1 to n
Yi = insert(Yi-1, y(i, n))
Прежде чем последовать дальше, надо определить несколько терминов.
местоположение (locus) строки - узел, представляющий строку в суффиксном дереве.
расширение строки u - любая строка, для которой u является префиксом
расширенное местоположение строки u - местоположение самого длинного расширения u, представленное в суффиксном дереве
сокращенное местоположение строки u - местоположение самого длинного префикса u, представленное в суффиксном дереве
головаi - самый длинный префикс y(i, n), который является также префиксом y(j, n) для некоторого j < i. Таким образом, головаi - это самый длинный префикс y(i, n), чье расширенное местоположение находится в Yi-1.
хвостi - строка, такая, что y(i, n) = головаiхвостi. Условие, требующее наличия завершающего символа $, гарантирует, что хвостi не пуст.
Рассмотрим в качестве примера y = EWEW$. На рисунке 4.30 показаны разные стадии конструирования его суффиксного дерева. Чтобы вставить в дерево суффикс y(i,n), сначала находят расширенное местоположение головыi в Yi-1. Затем в случае необходимости, создается новый внутренний узел, представляющий головуi, и вставляется в бывший входной узел. Наконец, добавляется новое ребро из местоположения головыi к новому узлу, представляющему y(i,n). Y4, например, строится следующим образом. Новый суффикс, y(4, n) - это W$, голова4 - это W, префикс предыдущего суффикса WEW$, а хвост4 - это $. Ребро, соединяющее корень с местоположением WEW$ расщепляется, и вставляется новый узел для W, и наконец, добавляется ребро из этого нового узла к новому листу для суффикса W$.
Вместо того, чтобы хранить для каждого узла дерева саму подстроку, достаточно представить эту подстроку парой целых чисел, обозначающих ее начальную и конечную позиции в исходной строке. Или можно использовать начальную позицию и длину подстроки. Таким образом, отдельные узлы дерева можно представить парой индексов подстроки и двумя указателями узлов - один указывает на первого потомка узла, а второй - на его следующего брата (sibling). Это проиллюстрировано на рисунке 4.31, где нулевые указатели представлены 0. Для удобства на рисунке указаны подстроки для каждого узла, хотя на самом деле они не хранятся в узлах.
Y0 Y3
корень корень ----- EW ----- EWEW$
| |
| ------ EW$
|
------------------ WEW$
Y1 Y4
корень ----- EWEW$ корень ----- EW ----- EWEW$
| |
| ------ EW$
|
--------- W ----- WEW$
|
------ W$
Y2 Y5
корень ----- EWEW$ корень ----- EW ----- EWEW$
| | | |
------- WEW$ | | ------ EW$
| |
| -------- W ---- WEW$
| |
| ----- W$
-------------------- $
Рисунок 4.30: Этапы конструирования суффиксного дерева для EWEW$
(0, 0) * 0
|
|
|
v
(1,2) **-------------------------------> (2,2) **------------> (5,5) 0 0
EW | W |
| |
| |
v v
(1,5) 0 *-----> (3,5) 0 0 (2,5) 0 *-----> (4,5) 0 0
EWEW$ EW$ WEW$ W$
Рисунок 4.31: Реализация узлов для суффиксного дерева EWEW$
Когда расширенное местоположение головыi в Yi-1 найдено, необходимые преобразования дерева на шаге i могут быть выполнены за фиксированное время. Таким образом, если поиск расширенного местоположения также можно выполнить за фиксированное время, усредненное по всем шагам, то суффиксное дерево может быть построено за линейное по время, пропорциональное n. Для этого в структуре данных применяются вспомогательные суффиксные звенья, а их использование основывается на следующей взаимосвязи между головойi-1 и головойi.
Если головаi-1 = az для некоторого символа a и некоторой (возможно, пустой) строки z, то z является префиксом головыi. Это можно доказать следующим образом. Если головаi-1 = az, то  j < i, такой, что az является префиксом как y(i-1, n), так и y(j-1, n). Строка z в этом случае является префиксом, общим для y(i, n) и y(j, n), и, таким образом, по определению является префиксом головыi.
Из каждого внутреннего узла, являющегося местоположением az, для некоторого символа a и строки z, добавляется суффиксное звено к местоположению z. Обратите внимание, что второе никогда не содержится в поддереве, корнем которого является первое. Эти добавочные звенья позволяют проводить быстрый поиск на стадии i для расширенного местоположения головыi начиная с местоположения головыi-1, которое находят на предыдущем этапе. Реализация суффиксного дерева с суффиксными звеньями к внутренним узлам, а именно, местоположению EW и W, показана на рисунке 4.31.
Выполнение алгоритма основывается на том, что (1) в Yi, только суффикс головыi может не иметь подходящего суффиксного звена, и что (2) на шаге i посещалось обусловленное местоположение головыi в Yi-1 (то есть местоположение самого длинного префикса головыi в Yi-1). Сначала, при i = 1, эти два условия, очевидно, выполняются. На этапе i выполняются следующие три подшага:
I находят три строки u, v и w, такие, что:
головаii = uvw
если сокращенное местоположение строки головаi-1 в Yi-2 не является корнем, то оно является местоположением uv. В противном случае v = e.
|u| < 1, u = e, если головаi+1 = e
Так как головаi-1 = uvw, то, как было показано ранее, vw является префиксом головыi (согласно (c) u - не больше, чем один символ). Таким образом, головаi задается как vwz для некоторой (возможно, пустой) строки z. Теперь проверим, пуста ли строка v, с помощью следующих действий.
-----------------------------------------------------------
| суффиксное звено |
v |
(0, 0) * 0 |
| ----------------------------------------------- |
| | суффиксное звено | |
| | | |
v | v |
(1,2) * * * ------------------------------------> (2,2) * * *--------> (5, 5) 0 0
EW | W | $
| |
| |
v v
(1,5) 0 * -----> (3, 5) 0 0 (2,5) 0 * -----> (4,5) 0 0
EWEW$ EW$ WEW$ W$
Рисунок 4.32: Реализация узлов суффиксного дерева для EWEW$, показывающая суффиксные звенья
v = 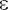 - корневой узел обозначается как с (местоположение v), и алгоритм переходит к шагу II.
v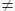 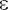- из b, местоположение uv в Yi-2 уже должно существовать. Согласно (1) суффиксное звено этого внутреннего узла должно быть определено в Yi-1, так как узел должен был быть добавлен до шага i - 1. Согласно (2), этот узел будет посещен на этапе i - 1. По его суффиксному звену мы затем проходим к внутреннему узлу c (местоположению v), и алгоритм переходит к шагу II.
II ('повторное сканирование'). Выше было показано, что головаi задается строкой vwz. По определению, тогда существует расширенное местоположение vw в Yi-1. Поэтому существует некоторая направленная вниз последовательность ребер из c (местоположение v), приводящая к местоположению некоторого расширения vw. Чтобы пересканировать w, порожденная c строка, скажем, e, такая, что e является местоположением расширения, скажем, vp, от v, присоединяется к первому символу w. Если |p| < |w|, то рекурсивное пересканирование q, где w = pq, начинается из узла e. Если, с другой стороны, |p| > |w|, то w является префиксом p, и расширенное местоположение vw найдено, пересканирование завершается, и по числу посещенных узлов затрачивается линейное время. В местоположении vw создается новый внутренний узел, если его еще там нет, что может быть только в случае z = 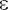. Местоположение vw обозначается d, и алгоритм переходит к шагу III.
III ('сканирование') Если суффиксное звено местоположения uvw (то есть, головаi-1) не определено, то его устанавливают так, чтобы оно указывало на узел d, гарантируя таким образом истинность (1). Затем предпринимается нисходящий поиск, начинающийся с d, для нахождения расширенного местоположения vwz (то есть, головыi). При повторном сканировании длина w известна, так как эта строка уже сканировалась, в то время при сканировании длина z неизвестна. Поэтому нисходящий поиск диктуется символами хвостаi-1 (префиксом которого является z) по одному слева направо. Когда нисходящий поиск больше не может продолжаться, находится расширенное местоположение vwz. Предыдущий узел, встретившийся во время этого путешествия, является сокращенным местоположением головыi, что гарантирует истинность (2). При необходимости создается новый внутренний узел, который будет местоположением vwz. Затем добавляется новое ребро из местоположения vwz к новому листу, представляющему суффикс y(i, n), и этап i завершается.
Для иллюстрации процесса МакКрейт приводит следующий пример. Рассмотрим шаг 14 при построении суффиксного дерева для y = BBBBBABABBBAABBBBB$. На рисунке 4.33 показано дерево Y13, в котором листья помечены соответствующим значением i для суффикса y(i, 19), который они представляют, и включены соответствующие суффиксные звенья. На шаге 14 в Y13 вставляется суффикс y(14, 19), а именно, BBBBB$. Первоначально, uv назначается значение AB, так как это строка, представляемая сокращенным местоположением головы13 в Y12, так что u = A, а v = B. Значение головы13 (uvw) равно ABBB, так что w должна быть равна BB. В I, v является непустой, так что суффиксное звено из местоположения uv (AB) проводится к узлу c (местоположению B). Отсюда w пересканируется на этапе II, встречая один промежуточный узел e и заканчивая узлом d, местоположением BBB. На этапе III добавляется новое суффиксное звено из местоположения головы13 к узлу d, и затем производится нисходящее сканирование из d, использующее символы хвоста13 (BB$), находя, что z = BB. Затем в качестве местоположения uwz (головы14) создается новый узел, которым в данном случае является BBBBB, и вставляется во входящее ребро расширенного местоположения uwz (листа для y(1, 19)). Наконец, добавляется новое ребро из местоположения BBBBB к новому листу, представляющему суффикс y(14, 19).
Для шага i обозначим через resi самый короткий суффикс (то есть wz хвостi) в операции пересканирования. Для каждого промежуточного узла e, посещенного при пересканировании w, p - это непустая строка, встречающаяся в resi, но не в resi+1. Для каждого промежуточного узла, минимальной длиной p является 1, поэтому максимальной длиной resi+1 является |resi| - inti, где inti является числом промежуточных узлов, встреченных в процессе пересканирования на этапе i. Таким образом, общее число промежуточных узлов, посещенных в процессе пересканирования, составляет 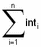 , что сверху ограничено n. Кроме того, на этапе i, число символов, которые необходимо просмотреть для локализации головыi, то есть |z|, равно |головаi| - |головаi-1| + 1. Для всего алгоритма это в итоге дает
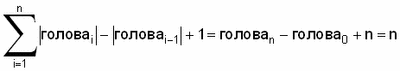
Вышеизложенное показывает, что операции пересканирования и сканирования всего процесса занимают время, линейное по n. Кроме того, ранее было показано, что каждый из n этапов алгоритма выполняется за фиксированное время, за исключением времени, которое требуется на пересканирование и сканирование. Таким образом, общее время, требуемое алгоритмом, линейно по n. Кроме того, время работы алгоритма линейно по размеру алфавита y, так как каждый узел может порождать до  узлов, для алфавита  .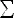
Представленная на рисунке 4.32 реализация дерева эффективна по памяти, однако приводит к медленному поиску. В качестве компромисса между требованиями памяти и приспособленностью к быстрому поиску, МакКрейт предложил реализацию, в которой ребра дерева кодируются как входы в хеш-таблице (используя алгоритм хеширования Лампсона (смотрите упражнение 6.4.13 Кнута, 1973).
Описав построение суффиксного дерева, мы теперь можем перейти к исследованию того, как эта структура данных используется для решения задачи самой длинной повторяющейся подстроки. Очевидно, что самая длинная подстрока, представляемая внутренним узлом Y, является самой длинной повторяющейся подстрокой y. Таким образом, достаточно проследить максимальную длину подстрок внутренних узлов в процессе построения дерева, которое, как мы уже видели, может быть выполнено за линейное время для фиксированного алфавита.
root ----- A ----- 12
| | ---------------
| ------ AB ----- 6 ' |
| ' | ' |
| suffix ' | ' |
| link ' ------ ABBB ----- 8 |
| ' (head_13) | |
| | ------ 13 |
| | |
| v |
------- B -----BA ----- 11 |
(node c) | | |
| ------ BAB ------ 5 |
| | |
| -------- 7 |
| |
| (node e) |
------ BB ----- BBA ----- 10 |
| | |
| ------- 4 |
| |
| --------------------
| '
| '
| |
| v
------ BBB ------ BBBA ----- 9
(node d) | |
| ------- 3
|
|
-------- BBBB ----- 2
|
------- 1
Рисунок 4.33: Y13 для строки BBBBBABABBBAABBBB$
корень ----------- AB ------ 11
/ | \ |
| | | -------- ABC ----- 2
| | | |
| | | ---------- 7
| | |
| | ----- B ------ 12
| | |
| | ------- BC -------- 3
| | |
| | ---------- 8
| |
| --------------------- C --------- 4
| |
| ---------- 9
|
-------------------------- 1, 5, 6, 10, 13, 14, 15
Рисунок 4.34: Суффиксное дерево для строки PABCQRABCSABTU$
Суффиксное дерево для строки y = PABCQRABCSABTU$ из предыдущего примера показано на рисунке 4.34. Здесь снова листья помечены соответствующими значениями i их суффиксов y(i, 15). Кроме того, все листья, не имеющие другого родителя, кроме корневого узла, были сгруппированы вместе в конце отдельного ребра. Из рисунка можно видеть, что ABC является самой длинной подстрокой, представляемой внутренним узлом, и, таким образом, самой длинной повторяющейся подстрокой y.
Аналогично можно определить самую длинную общую подстроку двух строк x и y, за время O(m + n) для фиксированного алфавита. В этом случае строится суффиксное дерево для строки x#y$, где символы # и $ не принадлежат алфавиту, строками над которым являются x и y. И снова, требуемый результат дается подстрокой максимальной длины, представляемой внутренним узлом суффиксного дерева.
И наконец, подход Бейкера [Baker, 1992] к задаче нахождения всех максимальных повторяющихся подстрок входной строки, более длинных, чем некоторое заранее заданное пороговое значение, использует просмотр суффиксного дерева строки. Подстрока, скажем, u, представляемая самым низким общим предком двух листьев в Y, является самым длинным общим префиксом двух суффиксов, представляемых этими листьями. Таким образом, она является подстрокой, появляющейся в двух разных местах с различным правым контекстом во входной строке. Чтобы определить, является ли u самой длинной повторяющейся подстрокой, осталось установить, различаются ли левые контексты ее двух вхождений в y. Если нет, значит u является всего лишь суффиксом некоторой более длинной повторяющейся подстроки.
Требуемая проверка левых контекстов может быть выполнена путем рекурсии по дереву, построением списком суффиксов, сгруппированных по левому контексту, и сравнением этих списком. Для каждого внутреннего узла создаются списки позиций суффиксов, представляемых листьями в поддереве, корнем которого является данный внутренний узел и имеющих одинаковый левый контекст. Максимальные повторения затем идентифицируются путем перечисления в каждом поддереве пар позиций из пар списков с различным левым контекстом. Например, рассмотрим суффиксное дерево для строки PABCQRABCSABTU$ (рисунок 4.34). Ища максимальные повторения длины 2 или более, мы обнаруживаем, что AB является максимальной повторяющейся подстрокой (левым контекстом y(11, 15) является S, а у y(2, 15) и y(7, 15) - P и R, соответственно); а BC нет (левым контекстом как для y(3, 15), так и для y(8, 15) является A). Если ограничиться только теми внутренними узлами, которые представляют подстроки, более длинные, чем заданный порог, просмотр дерева можно выполнить за время r, линейное по числу найденных пар максимальных повторений. С учетом времени на его построение, суффиксное дерево дает общую временную сложность O(n+r) для фиксированного алфавита. Затраты памяти те же, что и у суффиксного дерева, которые являются линейными по n. Кроме того, Бейкер расширил свой подход, чтобы находить параметризованные совпадения - это может использоваться, например, для идентификации похожих кусков кода в больших компьютерных программах.
8 8 8
| |
*
Обратная связь