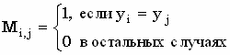
Наивный подход к задаче отыскания самой длинной повторяющейся подстроки для текстовой строки y может быть основан на матрице совпадений M размерности n * n. Элементы этой матрицы определяются следующим образом: Такая матрица симметрична относительно главной диагонали. Поэтому надо вычислить только элементы над ней или под ней. Диагонали из смежных '1', за исключением главной, представляют повторения в строке y, там-то и нужно искать максимальные повторяющиеся подстроки. Вот пример матрицы совпадений для строки PABCQRABCSABTU   j 1 2 3 4 5 6 7 8 9 10 11 12 13 14 i   P A B C Q R A B C S A B T U 1 P 1 0 0 0 0 0 0 0 0 0 0 0 0 0 2 A 0 1 0 0 0 0 1 0 0 0 1 0 0 0 3 B 0 0 1 0 0 0 0 1 0 0 0 1 0 0 4 C 0 0 0 1 0 0 0 0 1 0 0 0 0 0 5 Q 0 0 0 0 1 0 0 0 0 0 0 0 0 0 6 R 0 0 0 0 0 1 0 0 0 0 0 0 0 0 7 A 0 1 0 0 0 0 1 0 0 0 1 0 0 0 8 B 0 0 1 0 0 0 0 1 0 0 0 1 0 0 9 C 0 0 0 1 0 0 0 0 1 0 0 0 0 0 10 S 0 0 0 0 0 0 0 0 0 1 0 0 0 0 11 A 0 1 0 0 0 0 1 0 0 0 1 0 0 0 12 B 0 0 1 0 0 0 0 1 0 0 0 1 0 0 13 T 0 0 0 0 0 0 0 0 0 0 0 0 1 0 14 U 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Из приведенной выше матрицы можно видеть, что максимальными повторяющимися подстроками в данном примере являются ABC, с вхождениями y(2, 4) и y(7, 9), и AB, с вхождениями y(2, 3), y(7, 8) и y(11, 12). Легко выбрать более длинную из них, а именно, ABC. Как уже упоминалось, поскольку матрица симметрична, достаточно вычислить элементы над главной диагональю, M(1...n-1,i+1...n), то есть всего n(n-1)/2 элементов. Таким образом, оценивание матрицы требует времени, пропорционального O(n2).  8  Комментарии к статье  8 8  Обсудить в чате