8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
|
 |
Приложение А: Вычисление гамма-функции - Программирование от RIN.RU
|
Приложение А: Вычисление гамма-функции
Гамма-функция, задаваемая соотношением
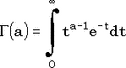 , ,
входит в нормирующий множитель практически во все функции распределения. Поэтому, естественно, важно уметь ее вычислять. Трудность, однако, в том, что эта функция очень быстро растет: ведь для нее выполнено соотношение 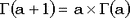 , т.е. для целых аргументов она растет как факториал, и не медленнее для дробных. , т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.
Быстрый рост чисел, с которыми приходится оперировать, необходимо учитывать и при вычислении собственно функций распределения. Скажем, вычисляя гамма-распределение, мы должны помнить о том, что неполная гамма-функция, нормирующим множителем для которой является 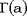 , при большом аргументе становится близкой к , при большом аргументе становится близкой к 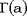 . т.е. тоже большой. Поэтому, не удается разделить вычисления - сначала вычислить неполную гамма-функцию, потом полную, а потом поделить одну на другую. Приходится изобретать уловки, позволяющие справиться с ситуацией. . т.е. тоже большой. Поэтому, не удается разделить вычисления - сначала вычислить неполную гамма-функцию, потом полную, а потом поделить одну на другую. Приходится изобретать уловки, позволяющие справиться с ситуацией.
Стандартная 'волшба' в подобных случаях - разделить вычисляемую функцию на произведение 'трудной' и легкой частей, где 'трудная' часть является произведением двух или большего числа быстро растущих сомножителей, и вычислять не саму 'трудную' часть, а логарифм от нее.
Вот и пример.
При x < a+1 для вычисления функции гамма-распределения 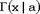 мы используем разложение мы используем разложение
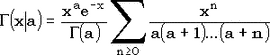 , ,
распадающееся на 'простую' часть 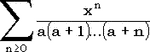 , при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и 'трудную', которую мы вычисляем как , при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и 'трудную', которую мы вычисляем как  . При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный 'трудный' сомножитель. . При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный 'трудный' сомножитель.
Другой пример.
Вычисляя бета-распределение 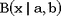 при небольших x, мы используем цепную дробь при небольших x, мы используем цепную дробь
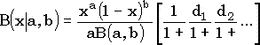 . .
И снова разложение распадается, и 'трудную' часть мы вычисляем как 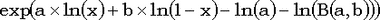 . И снова нужно уметь вычислять логарифм гамма-функции, поскольку . И снова нужно уметь вычислять логарифм гамма-функции, поскольку 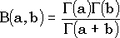 . .
В нижеследующих кодах используется асимптотическое разложение логарифма гамма-функции, которое (к сожалению, в недостаточно полном виде) можно найти в горячо рекомендуемом справочнике по специальным функциям М.Абрамовица и И.Стигана:
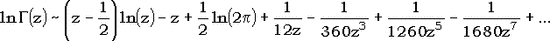
Когда аргумент z достаточно велик, его первые 20 членов дают около 50 верных знаков, если не учитывать ошибки, вызываемые конечной разрядностью. Отражением асимптотического характера ряда в кодах является увеличение слишком малого аргумента: если z меньше некоей границы (в данных кодах 7), он увеличивается, причем для корректировки используется упомянутое выше соотношение 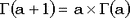 . .
1 2
8 8 8
| |
|
|





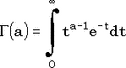 ,
,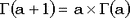 , т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.
, т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.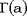 , при большом аргументе становится близкой к
, при большом аргументе становится близкой к 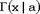 мы используем разложение
мы используем разложение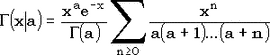 ,
,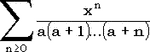 , при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и 'трудную', которую мы вычисляем как
, при работе с которой мы не сталкиваемся с слишком большими числами (факториал в знаменателе растет быстрее степени), и 'трудную', которую мы вычисляем как  . При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный 'трудный' сомножитель.
. При x > a+1, для вычисления гамма-распределения используется разложение в цепную дробь, куда входит аналогичный 'трудный' сомножитель.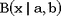 при небольших x, мы используем цепную дробь
при небольших x, мы используем цепную дробь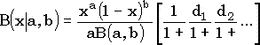 .
.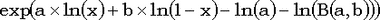 . И снова нужно уметь вычислять логарифм гамма-функции, поскольку
. И снова нужно уметь вычислять логарифм гамма-функции, поскольку 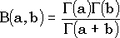 .
.