| Обозначение | 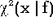 | | Область значений | 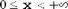 | | Параметры | f - параметр формы, целое положительное число; его часто называют числом степеней свободы. | | Плотность (функция вероятности) | 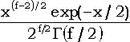 , где , где 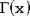 - гамма-функция - гамма-функция | Математическое
ожидание | f | | Дисперсия | 2f | | Функция распределения | Не выражается в элементарных функциях |
Связь с другими распределениями
Хи-квадрат с f степенями свободы совпадает с гамма-распределением с параметром масштаба 2 и параметром формы f/2. То же распределение можно получить, удвоив случайную величину, подчиняющуюся гамма-распределению с параметром масштаба 1 и параметром формы f/2: 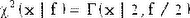 . .
Это соотношение позволяет вычислять функцию распределения хи-квадрат.
Если 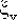 и и 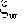 - независимые случайные величины, распределенные как хи-квадрат с v и w степенями свободы соответственно, то случайная величина - независимые случайные величины, распределенные как хи-квадрат с v и w степенями свободы соответственно, то случайная величина 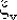 / /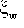 подчиняется F-распределению с v и w степенями свободы. подчиняется F-распределению с v и w степенями свободы.
Если случайная величина 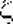 имеет F-распределение с v и имеет F-распределение с v и 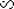 степенями свободы, то случайная величина степенями свободы, то случайная величина 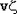 распределена как хи-квадрат с v степенями свободы. распределена как хи-квадрат с v степенями свободы.
Если случайная величина 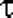 подчиняется T-распределениюСтьюдента с f степенями свободы, а подчиняется T-распределениюСтьюдента с f степенями свободы, а 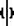 - стандартному нормальному распределению, причем - стандартному нормальному распределению, причем 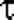 и и 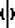 независимы, то случайная величина независимы, то случайная величина 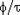 распределена как хи-квадрат с f степенями свободы. распределена как хи-квадрат с f степенями свободы.
Распределение хи-квадрат с f степенями свободы связано с распределением Пуассона с параметром x/2 следующим соотношением: 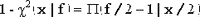
Распределение хи-квадрат с f степенями свободы совпадает с распределением суммы квадратов f независимых случайных величин, распределенных нормально с параметрами 0 и 1.
При f > 30 случайная величина 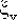 , распределенная как хи-квадрат с f степенями свободы, распределена приблизительно так же, как поделенный пополам квадрат нормальной случайной величины , распределенная как хи-квадрат с f степенями свободы, распределена приблизительно так же, как поделенный пополам квадрат нормальной случайной величины 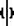 с единичной дисперсией и средним с единичной дисперсией и средним 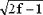 . .
Пусть даны n независимых случайных величин 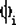 , i=1..n, распределенных нормально с параметрами , i=1..n, распределенных нормально с параметрами 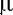 и и 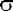 . Сумма квадратов их отклонений от среднего арифметического, деленная на . Сумма квадратов их отклонений от среднего арифметического, деленная на 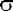 2,распределена как хи-квадрат с n-1 степенями свободы. То же самое по другому. Если 2,распределена как хи-квадрат с n-1 степенями свободы. То же самое по другому. Если 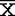 и s2 определить стандартным образом, то и s2 определить стандартным образом, то 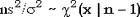
Генерация случайных чисел
Если ri распределены равномерно на [0,1], а 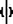 подчиняется стандартному нормальному распределению, то при четных f случайная величина распределена как хи-квадрат с f степенями свободы, а при нечетных f так распределена величина подчиняется стандартному нормальному распределению, то при четных f случайная величина распределена как хи-квадрат с f степенями свободы, а при нечетных f так распределена величина 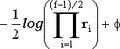 . Случайная величина . Случайная величина 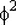 распределена как хи-квадрат с одной степенью свободы. распределена как хи-квадрат с одной степенью свободы.
Вычисление функции распределения и ее квантилей
Распределение хи-квадрат с f степенями свободы совпадает, как уже говорилось выше с гамма-распределением с параметром масштаба 2 и параметром формы f/2: 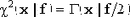 . Это соотношение и использовано в приводимых ниже кодах. . Это соотношение и использовано в приводимых ниже кодах.
1 2
8 8 8
| |








