8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
|
 |
Распределение Стьюдента - Программирование от RIN.RU
|
Распределение Стьюдента
Другое название - T-распределение
| Обозначение | 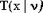 | | Область значений | 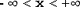 | | Параметры | Параметр формы 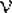 , число степеней свободы, целое положительное число , число степеней свободы, целое положительное число | | Плотность (функция вероятности) | 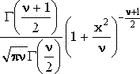 | | Математическое ожидание | 0 | | Дисперсия | 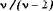 , , 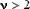 | | Функция распределения | Не выражается в элементарных функциях |
Связь с другими распределениями
Случайная величина 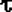 , имеющая распределение Стьюдента с , имеющая распределение Стьюдента с 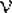 степенями свободы, следующими соотношениями связана с независимыми случайными величинами степенями свободы, следующими соотношениями связана с независимыми случайными величинами 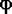 , , 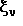 и и 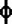 имеющими соответственно F-распределение с степенями свободы 1 и имеющими соответственно F-распределение с степенями свободы 1 и 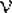 , распределение хи-квадрат с , распределение хи-квадрат с 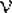 степенями свободы и нормальное с параметрами 0 и 1: степенями свободы и нормальное с параметрами 0 и 1:
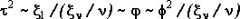
Кроме того, 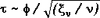 . .
При 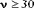 распределение Стьюдента достаточно для практических целей близко к нормальному распределению. распределение Стьюдента достаточно для практических целей близко к нормальному распределению.
Пусть даны n независимых случайных величин, распределенных нормально с параметрами 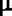 и и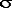 . Определим случайные величины . Определим случайные величины 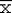 и и 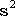 обычным образом. Тогда случайная величина обычным образом. Тогда случайная величина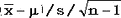 подчиняется T-распределению с n степенями свободы. На этом подчиняется T-распределению с n степенями свободы. На этом
свойстве основан одновыборочный T-критерий.
Пусть даны два набора из n1 и n2 случайных величин, распределенных нормально с параметрами 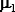 , , 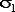 и и 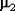 , , 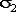 соответственно. Определим случайные величины соответственно. Определим случайные величины 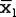 , , 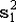 и и 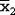 , , 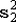 обычным образом. Тогда случайная величина обычным образом. Тогда случайная величина
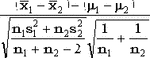
подчиняется T-распределению с n1+n2-2 степенями свободы. На этом свойстве основан двухвыборочный T-критерий.
Вычисление функции распределения и ее квантилей
Выше указано соотношение, связывающее распределение Стьюдента с F-распределением, которое, в свою очередь, является частным случаем бета. Это и дает нам способ вычисления функции распределения Стьюдента.
1 2
8 8 8
| |
|
|








