В последовательности испытаний Бернулли с вероятностью успеха p количество y испытаний вплоть до x-го успеха (включая и этот успех) подчиняется распределению Паскаля с параметрами x и p. Обозначение C(y|x,p) Область значений 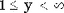, число испытаний, целое Параметры x - число успехов, целое положительное число p - вероятность успеха, 0 < p < 1 Плотность (функция вероятности) 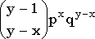Математическое ожидание x/p Дисперсия xq/p2 Функция распределения Не выражается в элементарных функциях Связь с другими распределениями Имеется следующее соотношение, связывающее распределение Паскаля с биномиальным: 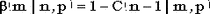. Сумма k независимых случайных величин yi, имеющих распределение Паскаля с параметрами p и xi, также подчиняется распределению Паскаля с параметром x = x1 + : + xk. Генерация случайных чисел Случайное число, соответствующее распределению Паскаля с параметрами p и x, можно получить, просуммировав x независимых случайных чисел, распределенных геометрически с параметром p. О том, как получить геометрическое распределение из равномерного см. в разделе о геометрическом распределении. Вычисление функции распределения и ее квантилей Ну, конечно, нужно воспользоваться связью с биномиальным распределением.  8  Комментарии к статье  8 8  Обсудить в чате