8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
|
 |
Отрицательное биномиальное распределение - Программирование от RIN.RU
|
Отрицательное биномиальное распределение
В последовательности испытаний Бернулли с вероятностью успеха p и вероятностью неудачи q=1-p число y неудач до x-го успеха имеет отрицательное биномиальное распределение.
| Обозначение | Y(y|x,p) - число неудач | | Область значений | 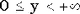 y - целое y - целое | | Параметры | x - число успехов, целое положительное число
p - вероятность успеха, 0 < p < 1 | | Плотность(функция вероятности) | 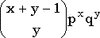 | | Математическое ожидание | xq/p | | Дисперсия | xq/p2 | | Функция распределения | 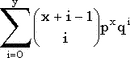 |
Связь с другими распределениями
В горячо рекомендуемом справочнике М.Абрамовица и И.Стигана ("Справочник по специальным функциям", М: Мир
1979, [26.5.26]) предлагается следующая связь отрицательного биномиального распределения с бета-распределением:
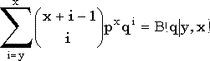 . .
Сумма k независимых случайных величин 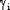 , i = 1..k, , i = 1..k,
распределенных геометрически с параметром p, подчиняется отрицательному биномиальному распределению с  . .
Генерация случайных чисел
Метод браковки
Берется последовательность независимых случайных чисел, равномерно распределенных на [0,1]. Среди них подсчитывается количество чисел, меньших p, и количество чисел, больших p. В тот момент, когда количество y чисел, меньших p,
впервые станет равным x, количество чисел, больших p, даст случайное число, подчиняющееся отрицательному биномиальному распределению .
Использование геометрического распределения
Если значение p мало, быстрее может оказаться суммирование x независимых геометрически распределенных случайных величин 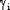 , i=1..x: случайная величина , i=1..x: случайная величина 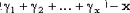 имеет отрицательное биномиальное распределение. Случайные величины имеет отрицательное биномиальное распределение. Случайные величины 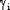
получаются из ri, равномерно распределенных на [0,1], согласно следующей формуле: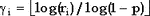 , где , где 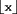 - значение x, округленное в большую сторону до ближайшего целого числа. - значение x, округленное в большую сторону до ближайшего целого числа.
Вычисление функции распределения и ее квантилей
Проще всего, конечно, использовать указанную связь с бета-распределением. Как и для всех дискретных распределений вычисление квантилей объявляется бесполезным. Взамен предлагается найти вероятность успеха, когда известны количества неудач и
успехов, а также соответствующее значение функции распределения.
Для вычислений с помощью нижеследующих кодов потребуются файлы betaDF.h, betaDF.cpp (см. раздел о бета-распределении), а также logGamma.h, logGamma.cpp (см. приложение А).
8 8 8
| |
|
|





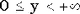 y - целое
y - целое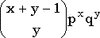
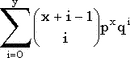
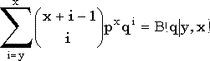 .
.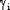 , i = 1..k,
, i = 1..k, .
.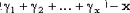 имеет отрицательное биномиальное распределение. Случайные величины
имеет отрицательное биномиальное распределение. Случайные величины 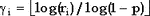 , где
, где 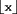 - значение x, округленное в большую сторону до ближайшего целого числа.
- значение x, округленное в большую сторону до ближайшего целого числа.