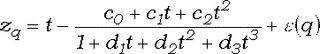8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
8
|
 |
Алгоритмы с конечной точностью - Программирование от RIN.RU
|
Алгоритмы с конечной точностью
Разложения, аппроксимирующие заданную функцию с некоей априори фиксированной точностью, можно получать множеством самых разных способов. Для получения полиномиальных приближений, например, одним из самых простых и мощных является, на мой взгляд, принадлежащий Ланцошу [5] процесс экономизации степенных рядов. Некоторые способы получения рациональных приближений описаны в работах [3, 6]; список литературы, посвященной этой проблематике, легко может быть продолжен.
В данном параграфе я приведу несколько таких широко известных разложений [10]. Разложения получены с помощью 'грубой силы': фиксировав вид аппроксимации, по значениям функции в нескольких точках можно оценить значения констант. Точность полученной аппроксимации оценивается сравнением истинных значений F(xi) и аппроксимирующих F*(xi)во многих точках. Успех всего предприятия определяется, конечно, нашей удачливостью в выборе вида аппроксимации.
Вот, например, как можно получить разложение A2.
Начнем с того, что фиксируем вид аппроксимации
(1) 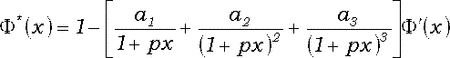
Перепишем (1) в более удобном виде
(2) 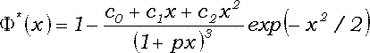
и положим
(3) 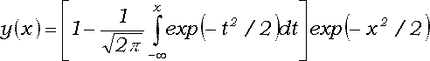
Вычислив y(x) в точках x0, x1, x2, x3, получаем четыре нелинейных уравнения для определения констант c0, c1, c2, c3, p:
(4) 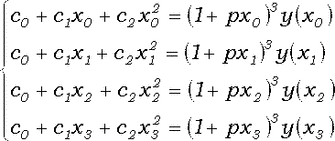
Полученная система уравнений совместна относительно неизвестных c0, c1, c2, c3 (константу p
пока считаем известной) тогда и только тогда, когда детерминант
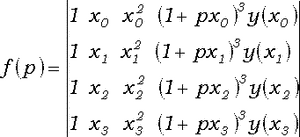
равен нулю. Разложив этот определитель по элементам правого столбца, получаем уравнение
(5) f(p)= A0(1+px0)3 + A1(1+px1)3 +
A2(1+px2)3 + A3(1+px3)3 = 0,
в котором A0, A1, A2 и A3 известны. Для определения корней этого уравнения используется какая-нибудь стандартная процедура, например, метод Ньютона. В работе [10] описаны причины, по которым в качестве p следует выбирать наименьший действительный корень уравнения (5).
Отбрасывая теперь любое (например, последнее) уравнение в системе (4), получаем линейную систему
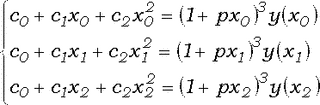
решив которую, получаем требуемые значения констант. Переход от разложения вида (2) к разложению A2 тривиален.
Алгоритмы, реализующие разложения A1-A4, приведены в приложении B; во всех этих алгоритмах для вычисления полинома использована схема Горнера.
A1: F(x) = 1-1/2(1 + a1x + a2x2 + a3x3 + a4x4)-4 + e(x),
|e(x)| < 2.5?10-4, 0 ? x < z1 = 3.72
a1 = 0.196854, a3 = 0.000344,
a2 = 0.115194, a4 = 0.019527;
F(x)
= 1 при x ? z1. A2: F(x) = 1- j(x) (b1t + b2t2 + b3t3) + e (x),
|e(x)| < 10-5, 0 ? x < z2 = 4.27
b1 = 0.4361836, b2 = -0.1201676, b3 = 0.937298;
F(x)
= 1 при
x ? z2.
A3: F(x) = 1- 1/2(1 + c1x+ c2x2+ c3x3+ c4x4+c4x5+
c4x6)-16+ e(x),
|e(x)| < 1.5?10-7,
0 ?x < z3 = 5.4
c1= 0.0498674370,
c4 = 0.0000380036,
c2= 0.0211410061, c5= 0.0000488906,
c3
= 0.0032776263, c6
= 0.0000053830;
F(x)
= 1 при
x ? z3.
A4: F(x)
= 1- j
(x) (d1t
+ d2t2
+ d3t3
+ d4t4
+ d5t5)
+ e
(x),
|e(x)|
< 7.5?10-8,
0 ?
x < z4
= 5.6,
d1
= 0.319381530,
d4 = -1.821255978,
d2
= -0.356563782, d5
= 1.330274429,
d3
= 1.781477937;
F(x)
= 1 при
x ? z4.
Приведу 'до кучи' аппроксимации, позволяющие находить квантили нормального распределения, т.е. значения zq, для которых F(zq) = q.
Z1: 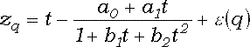 , ,
|e(x)| < 3*10-3, 0 ?q < 0.5,
a0= 2.30753,b1 = 0.99229,
a1= 0.27061, b2 = 0.04481.
Z2: 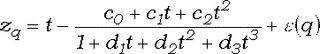
|e(x)| < 4.5*10-4, 0 ?q < 0.5,
c0= 2.515517,d1 = 1.432788,
c1= 0.802853, d2 = 0.189269,
c2
= 0.010328, d3 = 0.001308.
Первое из этих разложений было использовано в A-алгоритмах для оценки того xe, после которого можно
считать, что F(x) = 1.
Для вычисления F(x)с заранее фиксированной точностью легко придумать и другие алгоритмы; например, можно попросту посчитать интеграл - скажем, по формуле Симпсона. Здесь приведены наиболее экономные из всех известных мне способов.
8 8 8
| |
|
|





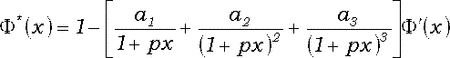
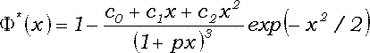
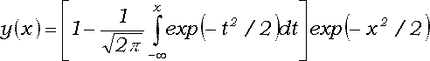
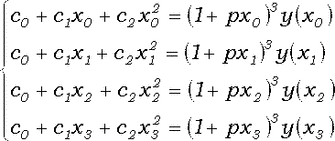
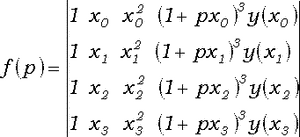
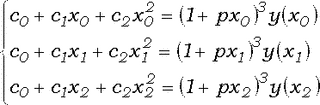
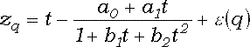 ,
,