Подробней о способах вычисления нормального распределения можно почитать в посвященной этому статье П.Н.Дубнера
Связь с другими распределениями
Пусть 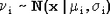 , i = 1..K - независимые нормально распределенные случайные величины. Тогда сумма , i = 1..K - независимые нормально распределенные случайные величины. Тогда сумма 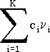 подчиняется нормальному распределению с параметрами подчиняется нормальному распределению с параметрами 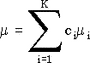 и и 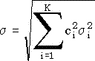 . .
В частности, сумма n независимых одинаково распределенных нормальных случайных величин 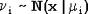 , i = 1..n, распределена нормально с средним n , i = 1..n, распределена нормально с средним n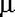 и стандартным отклонением и стандартным отклонением 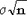 . .
Сумма квадратов независимых случайных величин 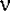 i, распределенных одинаково нормально с параметрами i, распределенных одинаково нормально с параметрами 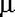 =0, =0,  =1, подчиняется распределению хи-квадрат с n степенями свободы: =1, подчиняется распределению хи-квадрат с n степенями свободы: 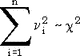 . .
Стандартное нормальное распределение является частным случаем гамма-распределения:
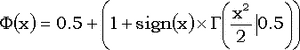 , ,
где
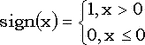 . .
Генерация случайных чисел
Пусть ri - независимы и распределены равномерно на [0,1]. Поскольку математическое ожидание ri равно 1/2, а дисперсия 1/12, то согласно центральной предельной теореме распределение суммы
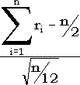
с ростом n стремится к нормальному с параметрами 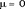 , , 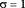 . Особенно простая формула получается, если взять n = 12. . Особенно простая формула получается, если взять n = 12.
Две независимые нормальные случайные величины 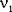 и и 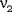 можно получить из двух независимых равномерно распределенных на [0,1] случайных величин r1 и r2 с помощью соотношений: можно получить из двух независимых равномерно распределенных на [0,1] случайных величин r1 и r2 с помощью соотношений:
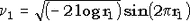 , , 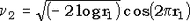 . .
Вычисление функции распределения и ее квантилей
Способам вычисления нормального распределения мы посвятили специальный текст, поэтому здесь ограничусь лишь двумя иллюстрациями.
Функция normalDF, позволяющая вычислять с "произвольной" точностью, использует указанную связь с гамма-распределением; чтобы эти коды работали, потребуются файлы loggamma.h и loggamma.cpp (см. Приложение А). Функция же inv_normalDF предназначена для вычисления квантилей нормального распределения с примерно тремя знаками. В ней использован алгоритм Z2 из $3 упомянутого текста про способы вычисления нормального распределения; заодно коды демонстрируют применение правила Горнера при вычислении полинома.
8 8 8
| |








