| Обозначение | 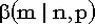 | | Область значений | 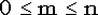 , где m - целое , где m - целое | | Параметры | n - целое положительное число (испытаний), 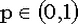 - параметр схемы Бернулли (вероятность "успеха"). Помните? величину 1-p принято обозначать буквой q. - параметр схемы Бернулли (вероятность "успеха"). Помните? величину 1-p принято обозначать буквой q. | | Плотность (функция вероятности) | Плотность дискретна: 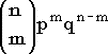 . .
Здесь 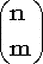 - число сочетаний из n элементов по m, причем - число сочетаний из n элементов по m, причем 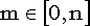 . . | | Математическое ожидание | np | | Дисперсия | npq | | Функция распределения | 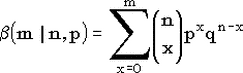 |
Полезные свойства
Как известно, функции биномиального и бета распределений связаны следующим соотношением: 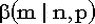 = =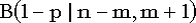 . .
Симметричности бета-распределения соответствует симметричность хвостов распределения биномиального: 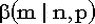 = = 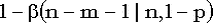 . .
Сумма k независимых случайных величин 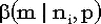 есть также биномиальная случайная величина есть также биномиальная случайная величина 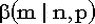 , ,
у которой 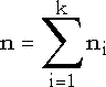 . .
Согласно теореме Муавра-Лапласа при 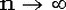 биномиальное распределение сходится к нормальному. Вот стандартная формулировка: если npq > 5 и 0.1 < p < 0.9, то биномиальное распределение сходится к нормальному. Вот стандартная формулировка: если npq > 5 и 0.1 < p < 0.9, то 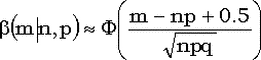 , где , где 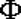 - стандартное нормальное распределение. - стандартное нормальное распределение.
В учебниках по статистике говорится, что если npq > 25, то эту аппроксимацию можно применять при произвольных значениях p. Если же значение p
мало, то биномиальное распределение принято аппроксимировать пуассоновским: 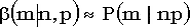 . Считается, что эту последнюю аппроксимацию следует применять при p< 0.1. . Считается, что эту последнюю аппроксимацию следует применять при p< 0.1.
Генерация случайных чисел
Берем n независимых случайных чисел, распределенных равномерно на отрезке [0,1]. Количество тех из них, которые меньше p, задают случайное число, подчиняющееся распределению 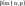 . .
Вычисление функции распределения и ее квантилей
Конечно, при вычислении кумулятивной функции распределения следует воспользоваться упомянутой связью биномиального и бета- распределения. Этот способ заведомо лучше непосредственного суммирования, когда n > 10.
В классических учебниках по статистике для получения значений биномиального распределения часто рекомендуют использовать формулы, основанные на предельных теоремах (типа формулы Муавра-Лапласа). Необходимо отметить, что с чисто вычислительной точки зрения ценность этих теорем близка к нулю, особенно сейчас, когда практически на каждом столе стоит мощный компьютер. Основной недостаток приведенных аппроксимаций - их совершенно недостаточная точность при значениях n, характерных для большинства приложений. Не меньшим недостатком является и отсутствие сколько-нибудь четких рекомендаций о применимости той или иной аппроксимации (в стандартных текстах приводятся лишь асимптотические формулировки, они не сопровождаются оценками точности и, следовательно, мало полезны). Я бы сказал, что обе формулы пригодны лишь при n < 200 и для совсем грубых, ориентировочных расчетов, причем делаемых 'вручную' с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Я не рассматриваю здесь задачу поиска квантилей: для дискретных распределений она тривиальна, а в тех задачах, где такие распределения возникают, она, как правило, и не актуальна. Если же квантили все-таки понадобятся, рекомендую так переформулировать задачу, чтобы работать с p-значениями (наблюденными значимостями). Вот пример: при реализации некоторых переборных алгоритмов на каждом шаге требуется проверять статистическую гипотезу о биномиальной случайной величине. Согласно классическому подходу на каждом шаге нужно вычислить статистику критерия и сравнить ее значение с границей критического множества. Поскольку, однако, алгоритм переборный, приходится определять границу критического множества каждый раз заново (ведь от шага к шагу объем выборки меняется), что непроизводительно увеличивает временные затраты. Современный подход рекомендует вычислять наблюденную значимость и сравнивать ее с доверительной вероятностью, экономя на поиске квантилей.
Поэтому в приводимых ниже кодах отсутствует вычисление обратной функции, взамен приведена функция rev_binomialDF, которая вычисляет вероятность p успеха в отдельном испытании по заданному количеству n испытаний, числу m успехов в них и значению y вероятности получить эти m успехов. При этом используется вышеупомянутая связь между биномиальным и бета распределениями.
Фактически, эта функция позволяет получать границы доверительных интервалов. В самом деле, предположим, что в n
биномиальных испытаниях мы получили m успехов. Как известно, левая граница двухстороннего доверительного интервала для параметра p с доверительным уровнем 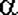 равна 0, если m = 0, а для равна 0, если m = 0, а для 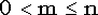 является решением уравнения является решением уравнения 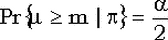 . .
Аналогично, правая граница равна 1, если m = n, а для 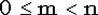 является решением уравнения является решением уравнения 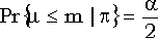 . .
Отсюда вытекает, что для поиска левой границы мы должны решать относительно  уравнение уравнение
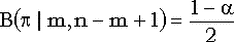
а для поиска правой - уравнение
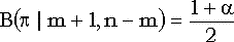
Они и решаются в функциях binom_leftCI и binom_rightCI, возвращающих верхнюю и нижнюю границы двустороннего доверительного интервала соответственно.
Хочу заметить, что если не нужна совсем уж неимоверная точность, то при достаточно больших n можно воспользоваться следующей аппроксимацией [Б.Л. ван дер Варден, Математическая статистика. М: ИЛ, 1960, гл. 2, разд. 7]:
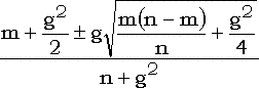 , ,
где g - квантиль нормального распределения.
Ценность этой аппроксимации в том, что имеются очень простые приближения, позволяющие вычислять квантили нормального распределения (см. текст о вычислении нормального распределения и соответствующий раздел данного справочника). В моей практике (в основном, при n > 100) эта аппроксимация давала примерно 3-4 знака, чего, как правило, вполне достаточно.
Для вычислений с помощью нижеследующих кодов потребуются файлы betaDF.h, betaDF.cpp (см. раздел о бета-распределении), а также logGamma.h, logGamma.cpp(см. Приложение А). Вы можете посмотреть также пример использования функций.
1 2
8 8 8
| |








